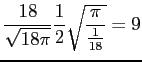Tag: integral

Kom til åbent hus i uge ?

Københavns Universitet holder åbent hus – men hvornår?

Mandag morgen stødte jeg på Nørreport på følgende (bare i plakatform):
KU - integral
Det var ikke lige en opgave jeg kunne løse i hovedet mandag kl. 7 om morgenen. Men i går aftes kunne jeg alligevel ikke lade være med at finde papir og blyant frem. Jeg kan godt mærke at det er længe siden jeg har rodet med integraler, men jeg kom da igennem (efter et enkelt opslag i Schaum’s).

Integralet der skal udregnes er

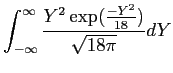
int_{-infty}^{infty}frac{Y^2exp(frac{-Y^2}{18})}{sqrt{18pi}}dY

Benyt at 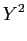Y^2 er en lige funktion.

2int_{0}^{infty}frac{Y^2exp(frac{-Y^2}{18})}{sqrt{18pi}}dY
frac{-9cdot 2}{sqrt{18pi}}int_0^{infty}Ycdotfrac{-Y}{9}expBig(frac{-Y^2}{18}Big)dY
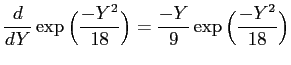
Brug frac{d}{dY}expBig(frac{-Y^2}{18}Big)=frac{-Y}{9}expBig(frac{-Y^2}{18}Big)

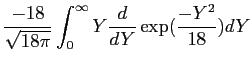
frac{-18}{sqrt{18pi}}int_0^{infty}Yfrac{d}{dY}exp(frac{-Y^2}{18})dY

Flyt differentiation fra exp til Y på bekostning af et fortegn. (Det virker i denne opgave, men der er vist nogle krav man egentlig skal tjekke om er opfyldt… mon ikke de er det?)

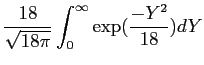
frac{18}{sqrt{18 pi}}int_0^{infty}exp(frac{-Y^2}{18})dY

Her måtte jeg søge hjælp i Schaum’s. Der skal bruges polære
koordinater og andre gode ideer for at vise at det faktisk gælder.

frac{18}{sqrt{18pi}}frac{1}{2}sqrt{frac{pi}{frac{1}{18}}}=9